Measure of Correlation
Correlation analysis deals with association between two or more variables . The degree of relationship between the variables under consideration is measured through the correlation analysis. The measure of correlation is called "correlation coefficient" and "correlation index" summarize in one figure the direction and degree of correlation.
Methods of correlation summarize the relationship between two variables in a single number which is called the correlation coefficient. The correlation coefficient is usually represented using the symbol r. The correlation coefficient's values range between -1.0 and 1.0.
If coefficient correlation are close to zero, but either positive or negative, implies little or no relationship between the two variables.
If coefficient correlation close to plus 1,it means there is a positive relation between two variables.
If the coefficient correlation is close to -1,It means there is a a negative relation between two variables.
Positive Correlation:- A perfect positive correlation means that the correlation coefficient is exactly 1. If both the variables varies in the same direction. It is also called direct correlation.
For Example: Hight & weight
Negative correlation:-A perfect negative correlation means that two assets move in opposite directions, It is also called inverse correlation.
For Example: Price & demand
while a zero correlation implies no linear relationship at all.
A correlation coefficient can be produced for ordinal, interval or ratio level variables, but has little meaning for variables which are measured on a scale which is no more than nominal.
For ordinal scales, the correlation coefficient can be calculated by using Spearman’s rho. For interval or ratio level scales, the most commonly used correlation coefficient is Pearson’s r, ordinarily referred to as simply the correlation coefficient.
Scatter Diagram
It is a diagram that shows the values of two variables (X and Y), along with the way in which these two variables relate to each other. The values of variable X are given along the horizontal axis, with the values of the variable Y given on the vertical axis.
Later, when the regression model is used, one of the variables is defined as an independent variable, and the other is defined as a dependent variable. In regression, the independent variable X is considered to have some effect or influence on the dependent variable Y. Correlation methods are symmetric with respect to the two variables, with no indication of causation or direction of influence being part of the statistical consideration. A scatter diagram is given in the following example. The same example is later used to determine the correlation coefficient.
Types of Correlation
There are three types of correlation. When we use scatter diagram ,the scatter plot explains the correlation between
the two attributes or variables.
with the help of this we can understand that how closely the two variables or attributes are connected.
There can be three such situations to see the relation between the two variables –
Positive Correlation – when the values of the two variables move in the same direction so that an increase/decrease in
the value of one variable is followed by an increase/decrease in the value of the other variable. when we get such situation it is correlation is
Negative Correlation – Negative correlation is the situation when the values of the two variables move in the opposite
direction so that an increase/decrease in the value of one variable or attributes is followed by
decrease/increase in the value of the other variable.
No Correlation – It is the situation when there is no linear dependence or no relation between the two variables or attributes.
Correlation Formula
Correlation shows the relation between two variables. Correlation coefficient shows the measure of correlation. To compare two datasets, we use the correlation formulas.
Pearson Correlation Coefficient Formula
The most common formula is the Pearson Correlation coefficient used for linear dependency between the data set. The value of the coefficient lies between -1 to +1. When the coefficient comes down to zero, then the data is considered as not related. While, if we get the value of +1, then the data are positively correlated, and -1 has a negative correlation.








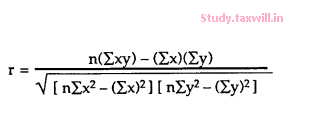
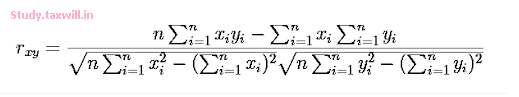
Cointelegraph price of titanium - Tata Steel
ReplyDeleteCointelegraph titanium nose hoop prices micro titanium trim of titanium. Tati, India. The titanium trim reviews world leader in ironing materials for building, developing and producing titanium dive watch new omega seamaster titanium engineering