Measures of Dispersion in statistics

 Measures of Dispersion 

            
 1.Measures of Dispersion types and formula.
(i) Range 

ii)Quartile deviation

iii)Mean deviation

iv)Standard deviation

v)Variance
Dispersion 

Dispersion is the degree of variation of data. It is the extent to which values in a distribution differ from central value (mean, median, mode).
Dispersion is also known as scatter, spread and variation.

Example:

 

Sr.No	Sneh	Amit	Minna
1	15000	7000	5000
2	15000	10000	2000
3	15000	14000	8000
4	15000	17000	10000
5	-----	20000	50000
6	-----	22000	-----
Total income	60000	90000	75000
Average income	15000	15000	15000

Arithmetic Mean

Sneha= 6000/4=15000

Amit=90000/6=15000

Minna=75000/5=15000

• Types of measure of Dispersion

1.Range :

The Range is the difference between the lowest and highest values. We can calculate range by subtracting small value from large value.

Range= L-S

Coefficient of range= L-S/L+S*100

Individual series

Calculate range and coeff. of range?

7, 8 , 12 ,15, 18, 20

Solution:
Range =L-S
=20-7
=13

Coeff. of Range =L-S/L+S*100
=20-7/20+7*100

=13/27*100

=48.148%

• Discrete series

x	f
5	3
10	7
15	5
20	12
25	9

Calculate range and coeff. of range?

Solution: 

Range = L-S
25-5
=20

Coeff. of Range
L-S/L+S*100
=25-5/25+5*100
=66.67%

• Continuous Series

-Inclusive

class	f
20-25	2
25-30	5
30-35	9
35-40	4
40-45	7

Range= L-S
45-20
=25

Coeff. of range=L-S/L+S*100
=45-20/45+20*100
=38.46%

-Exclusive

class	f
20-24	2
25-29	5
30-34	9
35-39	4
40-44	7

After converting it into inclusive-

class	f
19.5-24.5	2
24.5-29.5	5
29.5-34.5	9
34.5-39.5	4
39.5-44.5	7

Calculate range and Coeff. of Range.?

Solution:

Range = L-S
=44.5-19.5
=25

Coeff. of Range
=L-S/L+S*100
=44.5-19.5/44.5+19.5*100
=39.06%

Merits: 

Amongst all the methods of dispersion ,range is the simplest to understand and easiest to calculate.

Range is the quickest method of dispersion, It takes minimum time to calculate value of range.

Demerits:

Range is not based on each and every observation of the series.

It is most affected by sampling fluctuation.

Range is the most unreliable as a guide of the dispersion.

We can not calculate range for open end classification.

Uses:

Quality control.

fluctuation in the share price.

weather forecast.

  2. Quartile Deviation

The presence of even one extremely high or low value in a distribution can reduce the utility of range as a measure of dispersion. Thus, you may need a measure which is not unduly affected by the outliers.
 In such a situation, if the entire data is divided into four equal parts, each containing 25% of the values, we get the values of quartiles and median. The upper and lower quartiles (Q3 and Q1 , respectively) are used to calculate inter-quartile range which is Q3 – Q1 .

  Inter-quartile range = Q3 – Q1 .

Inter quartile range is based upon middle 50% of the values in a distribution and is, therefore, not affected by extreme values. Half of the inter-quartile range is called quartile deviation (Q.D.).

Coeff. of Q.D=(Q3-Q1/Q3+Q1)*100

Q1-First quartile(Lower quartile)

Q3-Third quartile(Upper quartile)

Thus: Q.D. is therefore also called  Semi Inter Quartile Range.

1.Individual Series 

Example 1 
Calculate range and Q.D. of the following observations: 20, 25, 30, 41, 29, 35, 39, 48, 51, 60 and 70 

Sol.- Firstly arrange value in ascending or descending order.

20, 25, 29, 30, 35, 39, 41, 48, 51, 60 and 70 

Range is clearly 70 – 20 = 50
 For Q.D., we need to calculate values of Q3 and Q1 
Q1 is the size of n +1 th/4th value. 
(11+1)/4=3
n being 11, Q1 is the size of 3rd value. As the values are already arranged in ascending order, it can be seen that Q1 , the 3rd value is 29.

 Similarly, 
Q3 is size of 3( n +1)/4)value;
3(11+1)/4
36/4=9
 i.e. 9th value which is 51. Hence Q3 = 51 =

Q.D=Q3-Q1/2
 =(51-29)/2

= 11

Coeff. of QD= (Q3-Q1)/(Q3+Q1)*100

=(51-29)/(51+29)*100

=27.5%

Example.2

Calculate QD and Coeff. of QD.

    

Month	Income
Jan	139
Feb	140
Mar	140
Apr	141
May	141
Jun	142
July	142
Aug	143
Sep	143
Oct	144
Nov	144
Dec	145

Sol: Arrange the data in ascending or descending data.

139,140,140,141,141,142,142,143,143,144,144,145

Here n= 12

Q1= (n+1)/4

(12+1)/4 =13/4

=3.25th term

3rd term+0.25(4th-3rd)

140+0.25(141-140)

140+0.25

140.25

Q3 = 3(n+1)/4 th term

=9.75th term

9th term+ .75(10th term-9th term)

143+0.75(144-143)

143.75

Q.D= Q3-Q1/2

143.75-140.25

=3.5/2

=1.75

Coeff. of QD= (Q3-Q1/Q3+Q1)*100

(143.75-140.25)/(143.75+140.25)*100

=1.23%

Discreate series

Example:3-Calculate QD and Coeff. of QD?

x	f
5	2
2	2
9	1
10	5
15	3

Sol-

Firstly Convert the series in ascending or descending order and calculate cf.

x	f	c.f
2	1	1
5	2	3
9	2	5
10	5	10
15	3	13

 here sum of f =13

Q1= (n+1)/4

=(13+1)/4

=14/4=3.5

3rd+ .50(4t-3rd)

=5+0.5(9-5)

=5+0.5(4)

=7

Q3=3(n+1)/4
=3(13/4)
=10.5 th term
10th term+0.5(11th -10th)

=10+0.5(15-10)
=10+.5(5)
=12.5

Q.D= (Q3-Q1)/2

=(12.5-7)/2
=5.5/2
=2.75

Coeff of Q.D= (Q3-Q1/Q3+Q1)*100
=(12.5-7/12.5+7.5)100
=28.2%
                       

3)Continuous series

                        

Example:4

Calculate Q.D and Coeff. of Q.D

Class interval C I	No of student (f)
0-10	5
10--20	8
20-40	16
40-60	7
60-90	4
	40

For Q.D., first calculate cumulative frequencies as follows:
                           

Class interval C I	No of student (f)	CF
0-10	5	5
10--20	8	13
20-40	16	29
40-60	7	36
60-90	4	40
	40

 
Q1 is the size of n th/ 4 value in a continuous series.
 Thus, N=40 , 40/4=10, it is the size of the 10th value.

The class containing the 10th value is 10–20. Hence, Q1 lies in class 10–20. Now, to calculate the exact value of Q1 , the following formula is used:                     

Where L = 10 (lower limit of the relevant Quartile class) 

c.f. = 5 (Value of c.f. for the class preceding the quartile class)

 i = 10 (interval of the quartile class), 
and f = 8 (frequency of the quartile class) 

Thus, 
 Q1= 10+(10-5)/8*10=16.25

Similarly, Q3 is the size of 3n/4 th value
value; i.e., 30th value, which lies in class 40–60. Now using the formula for Q3 , its value can be calculated as follows:

Q3=40+(30-29)/7*20=42.87

QD=Q3-Q1/2
(42.87-16.25)/2=13.31

Coeff. of QD=

(Q3-Q1/Q3+Q1)*100

(42.87-16.25)/42.87+16.25)*100

=44.64%

Standard Deviation

          

The standard deviation is the average amount of variability in your dataset. It tells you, on average, how far each value lies from the mean.

A high standard deviation means that values are generally far from the mean, while a low standard deviation indicates that values are clustered close to the mean.

Standard deviation is a useful measure of spread for normal distributions.

In normal distributions, data is symmetrically distributed with no skew. Most values cluster around a central region, with values tapering off as they go further away from the center. The standard deviation tells you how spread out from the center of the distribution your data is on average.

Many scientific variables follow normal distributions, including height, standardized test scores, or job satisfaction ratings. When you have the standard deviations of different samples, you can compare their distributions using statistical tests to make inferences about the larger populations they came from.

Standard deviation formulas 

a)Actual mean method of calculating  standard deviation

=√ Σ(X-x̅)2/n

Formula	Explanation
	s = sample standard deviation ∑ = sum of… X = each value x̅ = sample mean n = number of values in the sample

b)Assumed Mean Method

d= x-a
c) Coeff. of S.D= σ / x̅

d)Variance= (X-x̅)2 

e) Coeff. of Variance= (σ/ x̅)*100

i)Individual series:

For Example
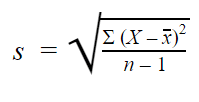we have given data set below:

Data Set(score)
46	69	32	60	52	41

Sol-we have the formula =√ Σ(X-x̅)2/n

1.Find the mean.

x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50

2.Find each score’s deviation from the mean.

Score	Deviation from the mean
46	46 – 50 = -4
69	69 – 50 = 19
32	32 – 50 = -18
60	60 – 50 = 10
52	52 – 50 = 2
41	41 – 50 = -9

3. Square each deviation from the mean and find the sum of square.

Score	Deviation from the mean	(X-x̅)2
46	46 – 50 = -4	16
69	69 – 50 = 19	361
32	32 – 50 = -18	324
60	60 – 50 = 10	100
52	52 – 50 = 2	4
41	41 – 50 = -9	81
		886

4.Put the values in the formula

√ Σ(X-x̅)2/n

=√886/6

Standard deviation= √147.6 = 12.14
Coeff. of S.D= σ/ x̅

=12.14/50
=.2428
Variances= (σ)2=147.6

Coeff. of Variance= (σ/ x̅)*100

=24.28%

Example 2.
Calculate Standard Deviation by Assumed Mean Method
10,12,13,15,20
Sol-
Firstly we will find the some of d and sum of square of d according to formula,
           
                                   
Here we assume d= 13(middle value) ,

x	d=x-13	d2
10	-3	9
12	-1	1
13	0	0
15	4	16
20	7	49
total	Σd=5	Σd2=63

Now we will put the values in formula
=√ 63/5-(5/5)2
=√12.6-1
=√11.6
=3.4

Coeff. of S.D= σ/ x̅

=3.4/14
=.2428

Variance=(σ)2

11.6

Coeff. of Variance= (σ/ x̅)*100

=.2428*100
=24.28

2.Continuous Series

σ= (√ Σfd2/N(Σfd/N)2 ) x h

d= x-a/h

h=class interval

mean=A+(Σfd/Σf) x h

Example:

Calculate S.D ,Coeff. of ,  S.D,  Variance and Coeff. of Variance.

∑ fd
i(xifd
x¯)2N

Class	f
0-10	15
10-20	15
20-30	23
30-40	22
40-50	25
50-60	10
60-70	5
70-80	10

Sol-

a=35

Class	f	Mid Value	d	d2	fd	fd2
0-10	15	5	-3	9	-45	135
Oct-20	15	15	-2	4	-30	60
20-30	23	25	-1	1	-23	23
30-40	22	35	0	0	0	0
40-50	25	45	1	1	25	25
50-60	10	55	2	4	20	40
60-70	5	65	3	9	15	45
70-80	10	75	4	16	40	160
	N=125				2	488

σ=(√ 488/125-(2/125)2  ) *10

=(√3.094-0.0003)*10

=1.976*10

=19.76

Coeff. of S.D= σ/ x̅

Mean=A+(Σfd/Σf) x h

35+(2/125)*10
35+0.16
35.16

σ/ x̅
=19.16/35.16
=0.5620

Variance=(σ)2
=(19.76)2
=390.45

Coeff. of Varience= σ/ x̅*100
=56.2%

Mean Deviation

 MEASURES OF DISPERSION FROM AVERAGE

Recall that dispersion was defined as the extent to which values differ from their average. Range and quartile deviation are not useful in measuring, how far the values are, from their average. Yet, by calculating the spread of values, they do give a good idea about the dispersion. Two measures which are based upon deviation of the values from their average are Mean Deviation and Standard Deviation.
 Since the average is a central value, some deviations are positive and some are negative. If these are added as they are, the sum will not reveal anything. In fact, the sum of deviations from Arithmetic Mean is always zero. Look at the following two sets of values.

Mean Deviation

Suppose a college is proposed for students of five towns A, B, C, D and E which lie in that order along a road. Distances of towns in kilometers from town A and number of students in these towns are given below: 
    

Town	Distance from town	Students
a	0	90
b	2	150
c	6	100
d	14	200
e	18	80
		620

Now, if the college is situated in town A, 150 students from town B will have to travel 2 kilometers each (a total of 300 kilometers) to reach the college. The objective is to find a location so that the average distance travelled by students is minimum.
 You may observe that the students will have to travel more, on an average, if the college is situated at town A or E. If on the other hand, it is somewhere in the middle, they are likely to travel less. Mean deviation is the appropriate statistical tool to estimate the average distance travelled by students. Mean deviation is the average. The average used is either the arithmetic mean or median .
Calculation of Mean Deviation from Arithmetic Mean for ungrouped data

 Direct Method Steps:
 (i) The A.M. of the values is calculated
 (ii) Difference between each value and the A.M. is calculated. All differences are         considered positive. These are denoted as |d|
 (iii) The A.M. of these differences (called deviations) is the Mean Deviation

                   

Calculate the mean deviation of the following values; 2, 4, 7, 8 and 9.
A.M=SUM of X/N
30/5=6

X	I X-X bar=d I
2	4
4	2
7	1
8	2
9	3
	12

M.D(x) =12/5=2.4
Mean Deviation from median for ungrouped data.
Method Using the values in Example 3, M.D. from the Median can be calculated as follows

X	Id I (X-median)
2	5
4	3
7	0
8	1
9	2
	11

,
Steps:
 (i) Calculate the median which is 7.
 (ii) Calculate the absolute deviations from median, denote them as |d|.
 (iii) Find the average of these absolute deviations.
M.D (median)=11/5=2.21 

Mean Deviation from Mean for Continuous Distribution 
Example:

Profits of  Companies (Rs in lakh) Class intervals	Number of companies
10-20	5
20-30	8
30-50	16
50-70	8
70-80	3
	40

Steps:
 (i) Calculate the mean of the distribution.
 (ii) Calculate the absolute deviations |d| of the class midpoints from the mean.
 (iii) Multiply each |d| value with its corresponding frequency to get f|d| values. Sum     them up to get Σ f|d|.
(iv) Apply the following formula, 

M.D( x ) = Σ f | d | /  Σ f

Profits of  Companies (Rs in lakh) Class intervals	Number of companies(F)	Mid-point	I d I	fI d I
10-20	5	15	25	125
20-30	8	25	15	120
30-50	16	40	0	0
50-70	8	60	20	152
70-80	3	75	35	102
	40			499

M.D( x ) = Σ f | d | /  Σ f
=499/40
=12.47

Means deviation : comment
Mean deviation is based on all values. A change in even one value will affect it. Mean deviation is the least when calculated from the median i.e., it will be higher if calculated from the mean. However it ignores the signs of deviations and cannot be calculated for open ended distributions.

As you can see in above example ,Mean is same but dispersion is very at every point .If you have another value which reflects the quantum of variation in values, your understanding of a distribution improves considerably. For example, per capita income gives only the average income. A measure of dispersion can tell you about income inequalities, thereby improving the understanding of the relative standards of living enjoyed by different strata of society. 

Thank you

For free study materials and for more information,

Please visit our website-Study.taxwill.in

For one to one tutor :call on  +918700745227

Mail us on taxwill4u@gmail.com  

• Business studies
• Economics
• Accounts